什么是仙人掌？

如果一个无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。

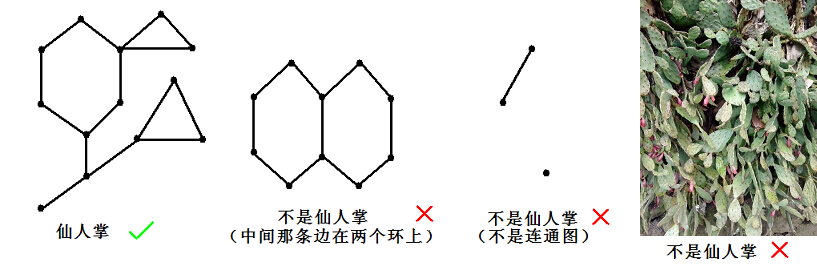
仙人掌的边数

考虑仙人掌的一棵生成树，有$n$个点和$n-1$条边

剩下的边为非树边，每条非树边对应了生成树上的一条路径， 且这些路径不重叠

最多有$n-1$条这样的路径，所以$n$个点的仙人掌最多有$2 n - 2$条边

仙人掌的结构

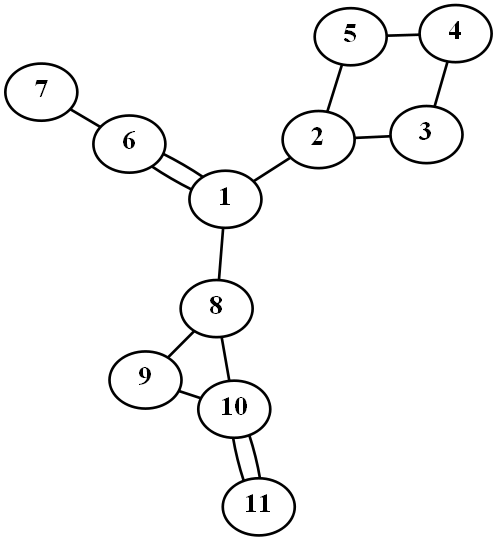
一棵根为1的仙人掌

一个结点的父亲可能是个结点，也可能是个环。 注意根节点没有父亲。 比如说，8号结点的父亲是1号结点，10号结点的父亲是环8-9-10，11号结点的父亲是环10-11 一个环的父亲为环上离根最近的结点 比如说，环8-9-10的父亲为8号结点，环10-11的父亲为10号结点

仙人掌的结构

一棵根为1的仙人掌

一个结点的儿子可能是个节点，也可能是个环 比如说，1号结点的儿子有2号结点、8号结点和环1-6 一个环的儿子为环上除去环的父亲以外的所有结点 比如说，环8-9-10的儿子为9号结点和10号结点

仙人掌的结构

一棵根为1的仙人掌

对于一个在环上的结点，我们定义它的父亲结点和母亲结点分别为环上与它相邻的两个结点 （请注意区分父亲和父亲结点） 比如说，在环2-3-4-5中，3号结点的父亲结点为2号结点，母亲结点为4号结点， 4号结点的父亲结点为3号结点，母亲节点为5号结点 从环的任意一个儿子出发，沿着父亲结点和母亲结点就能遍历整个环

如何遍历一棵仙人掌

• 从根开始dfs
• 假设当前在结点$x$，接下来要访问结点$y$

情况一

$y$还没有访问过

• 跟树上的情况一样处理, 只要将$y$的父亲设置为$x$

情况二

$y$已经访问过，且第一次访问$y$的时间早于第一次访问$x$的时间

• 说明我们发现了一个环，
  这个环的父亲为$y$，儿子为$x$到$y$路径上除去$y$的所有点


• 我们遍历这个环，并设置环上所有点的父亲结点和母亲结点

情况二

$y$已经访问过，且第一次访问$y$的时间早于第一次访问$x$的时间

一棵根为1的仙人掌

比如说，$x$是5号结点，$y$是2号结点 我们遍历整个环2-3-4-5，然后设置3,4,5号结点的父亲结点和母亲结点

情况三

$y$已经访问过，且第一次访问$y$的时间晚于第一次访问$x$的时间

一棵根为1的仙人掌

这说明，$y$在一个已经访问过的环上，可以无视这种情况

仙人掌上的简单DP

• 给一棵仙人掌，求直径。
• 直径的定义是，距离最远的两个点的距离。
  其中两个点的距离为它们之间的最短路径的长度。
• $n \le 10^5$

• 由于树也是仙人掌，我们先来考虑树上的情况
• 一个经典的做法是，随便选一个点，然后找到离它最远的点
  再从这个点开始，再找一次最远的点，这两个点之间的距离即为答案


• 这个做法在仙人掌上是错的

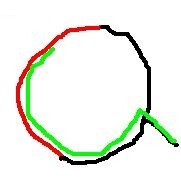
仙人掌上的简单DP

• 先以1号结点为根，dfs一遍，弄清仙人掌的结构
• 然后对于每个结点$x$，求出以$x$为根的子仙人掌的最大深度
  （以$x$为根的子仙人掌的定义是，删掉根到$x$的所有简单路径上的边之后，$x$所在的联通块）
• 然后用每个结点的不同儿子的最大深度+次大深度来更新答案
• 对于每个环，还需要用环上每对结点的子仙人掌最大深度的和加上这对结点的最短路来更新答案
• 很容易用单调队列来维护


• 也可以不用单调队列
• 按照从环的父亲往下走哪边距离近，把环分成两部分
• 每一部分内部的点对的最短路一定是在内部走
• 其他点对可以用前缀max和后缀max来解决

感觉水爆了？

mx的仙人掌

• 给一棵n个点的仙人掌和q个询问
• 每个询问给定一个点集，要求输出这个点集中距离最远的点对的距离
• 两个结点之间的距离为它们的最短路径长度
• $n \le 3 \times 10^5, q \le 3 \times 10^5, $ 点集中点的个数之和$ \mathrm{tot} \le 3 \times 10^5$
• 时间限制5s，内存限制512MB

树上的情况

• 由于树也是仙人掌，我们先来考虑树上的情况：
  “给定一棵树，每个询问给定一个点集，问这个点集中距离最远的点对的距离”


• 对询问的点集建一棵虚树，然后在虚树上DP即可

仙人掌上的情况

• 类比虚树，我们可以对询问的点集建一棵“虚仙人掌”


• 将询问点按dfs序排序，然后将相邻的结点的lca也加进虚仙人掌里
• 由于细节太多没法说清楚
• 可以参考 出题人的题解

我不会写虚仙人掌怎么办？

树上的情况的另一种做法

• 考虑对原树进行点分治
• 对于每一次分治，用不同子树中属于相同询问集合的结点之间的距离来更新答案
• 复杂度是$O(n \log n)$的（可以认为$q = O(n), \mathrm{tot} = O(n)$）

仙人掌上的情况

• 类比树的点分治，我们可以对仙人掌进行点分治


• 每次找一个点，使得删掉与这个点相连的边后，剩下的最大连通块大小最小
• 然后统计最短路经过这个点的点对，以及最短路经过这个点所在环的点对
• 然后对于每个连通块，递归进行分治
• 由于细节太多没法说清楚
• 可以参考 出题人的题解

我不会写仙人掌分治怎么办？

树上的情况的一种暴力

• 对于每个询问，进行一次树形DP
• 对于每个结点，求出这棵子树中的询问点到该结点的最大距离
• 然后用每个结点的不同子树的信息更新答案


• 有一个很显然的性质：
• 如果一个询问给了$k$个点，那么更新这个询问的答案的有效次数不超过$k-1$次！
• 于是对于所有询问，更新答案有效次数不超过$\mathrm{tot} - q$次！


• 我们可以对所有询问一起DP， 于是问题转化成，对于每个结点，快速找到需要更新答案的询问的编号
• 这相当于，维护很多数的集合，支持把其中两个合并， 并且在合并的时候输出它们的交集

• 启发式合并
• 每次将较小的集合中的所有元素插入较大的集合
• 由于要求交集，所以要快速判断一个集合中是否有某个元素
• 对每个集合开一个哈希表即可
• 时间复杂度是$O(n \log n)$的，空间复杂度是$O(n)$的


• 这个做法可以推广到仙人掌上
• 注意在环上更新答案时，需要将一些集合先合并然后再撤销这些合并操作, 更新完答案后，要将所有集合合并
  这两步的复杂度是一样的
• 所以时间复杂度还是$O(n \log n)$，空间复杂度还是$O(n)$，而且比虚仙人掌和仙人掌分治好写多了

动态仙人掌

• 给一棵仙人掌，要求支持加边、删边、询问两点之间的最短路上的最小边权， 还要支持对最短路上边权进行整体操作。
• 如果某个操作后某个联通块不是仙人掌，就不执行这个操作。
• $n \le 10^5$

link-cut cactus

• 类比link-cut tree，维护仙人掌的一个链剖分
• 保证access时沿最短路


• 如果没有环，跟link-cut tree的维护方法一样， 每个结点有个preferred-child，用实边连接起来，其他儿子用虚边连接

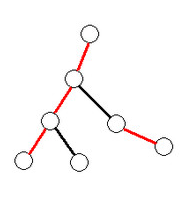
link-cut cactus

• 对于一个环，我们设它的父亲为$A$，preferred-child为$B$
• 我们将$A$和$B$最短路上的点用实边连起来
• 对于环上其他的结点构成的链，也用实边连起来，我们称这条链为额外链

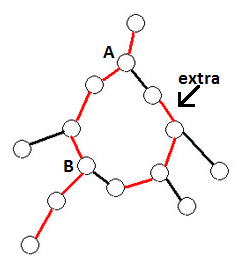
怎么维护边的信息？

• 在边上加个点！
• 注意环上的两条黑色边，我们将它直接接在额外链的两端来维护

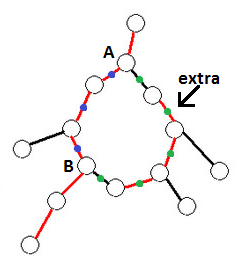
边界情况

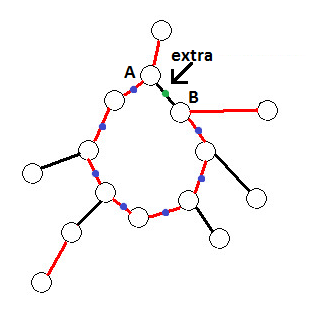
一种特殊情况

如图，上一次access了结点$A$，这会导致$A B$链上与$A$相连的边变为虚边 表示这条边的点还在$A B$链上的splay上

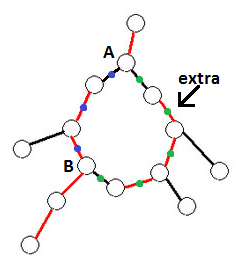
access操作

• 假设当前access到点$x$， 我们找到$x$在splay上的前一条边$e$
• 如果$e$不在环上，就跟link-cut tree一样处理


• 如果$e$在环上
• 首先将这个环的$A B$链的左右两端断开
  （要注意考虑特殊情况）
• 然后把$A B$链和额外链接起来，将$x$提到splay的根
• 选择较短的一边连回去，将另一边设置为额外链

换根操作

• 类似link-cut tree，可以在access某个结点后， 给根到结点的路径打翻转标记来换根


• 有没有漏掉什么神奇的地方？

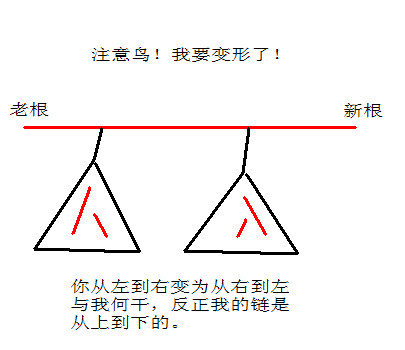
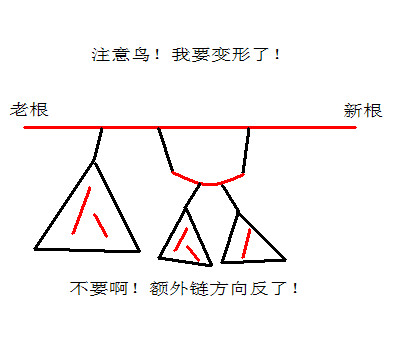
换根操作

• 这种情况下，环上的$A$结点和$B$结点的位置互换了，且额外链的方向反了
• 对于access到的每一个环，检查$A$结点和$B$结点在splay上的先后顺序， 如果反了，就将这个环的$A$结点和$B$结点互换，并给额外链打翻转标记

时间复杂度

• 结点和环的preferred-child的切换次数是均摊$O(n \log n)$的
• 所以复杂度的上界是$O(n \log ^ 2 n)$
• 实际运行速度也不是特别慢，在点数为$10 ^ 5$，操作数为$5 \times 10 ^ 5$时只要跑3s多

codechef PUSHFLOW

• 给一棵仙人掌，每条边有个容量
• 有$q$个操作，每个操作是修改一条边的容量，或询问两个点之间的最大流。
• $n \le 10^5, q \le 2 \times 10 ^ 5$

link-cut cactus的做法

• 用link-cut cactus维护这棵仙人掌
• 由于是要求最大流，我们只要维护路径上边的容量的最小值
• 对于每个环，我们将额外链的边的容量最小值加到$A B$链的每一条边的容量上
• 对于修改操作，换根、access以后直接修改即可
• 时间复杂度是$O(n \log ^ 2 n)$，由于常数太大在codechef上TLE了

link-cut tree的做法

• 对于某个环$C$，假设$C$上容量最小的边为$e$
• 考虑一个询问$(S, T)$，如果$S$到$T$的路径经过了环$C$， 那么在环$C$上一定有一条路径经过了$e$，另一条路径不经过$e$
• 经过$e$的那条路径的容量最小值一定是$e$的容量， 所以可以把$e$这条边从环$C$上断开，然后把$e$的容量加到环$C$的其他边上
• 对于修改操作，我们重新找到被修改的边所在的环上的容量最小的边， 然后进行几次link和cut即可
• 由于每个环都被删掉了一条边，所以我们维护的是仙人掌的一棵生成树， 只要用link-cut tree就行了
• 时间复杂度$O(n \log n)$，在codechef上AC毫无压力
  

动态仙人掌IV

• 给一棵仙人掌，要求支持加边、删边、对某两点之间最短路或某个子仙人掌进行修改或询问
• 根为$x$时，子仙人掌$y$的定义是，删掉$x$到$y$的所有简单路径上的边后，$y$所在的连通块
• 修改是将一条链或一个子仙人掌的点权加上一个数或修改为同一个数
• 询问的是一条链或一个子仙人掌的点权最大值、最小值、和

一个子问题

• 给一棵树，要求支持加边、删边、对某条路径或某个子树进行修改或询问


• Self-Adjusting Top Trees
• 大致思想是，在link-cut tree上
• 对每个结点用一棵splay来维护这个结点的所有子树的信息
• 标记的下传各种麻烦
• 由于不是重点不详细讲
• Tarjan 证明了这个算法的复杂度是$O(\log n)$的，虽然有$96$的常数

• 我们用link-cut cactus来维护仙人掌的形态
• 对于每个环，我们将环上的$B$点与额外链相连的边断开
  （要注意环上只有两个点的情况）
• 这样我们就得到了这棵仙人掌的一棵生成树，可以用Self-Adjusting Top Trees维护
• 在link-cut cactus的access操作时，会影响到$O(\log n)$个环的preferred-child
• 于是每次access操作会进行$O(\log n)$次Self-Adjusting Top Trees的link和cut操作，复杂度是均摊$O(\log ^ 2 n)$的


• 好像有点无聊？

动态仙人掌IV EXT

• 给一棵仙人掌，要求支持加边、删边、对某两点之间最短路或某个子仙人掌进行修改或询问
• 根为$x$时，子仙人掌$y$的定义是，删掉$x$到$y$的所有简单路径上的边后，$y$所在的连通块
• 修改是将一条链或一个子仙人掌的点权加上一个数或修改为同一个数
• 询问的是一条链或一个子仙人掌的第$k$大点权

一个子问题

• 给一棵树，要求支持加边、删边、对某条路径或某个子树进行修改或询问第$k$大点权
• Self-Adjusting Top Trees 不能用了！
  因为在Self-Adjusting Top Trees中，一个点的信息可能被统计了多次

一个子问题

• 考虑维护链和子树信息的另一种经典做法：dfs序
• 由于有链修改和询问第$k$大，维护dfs序的数据结构可以是块状链表
• 假设块状链表的块大小为$T$，那么在块状链表上一次分裂或合并操作需要$O(\log n + T)$的时间， 一次询问操作需要$O(\frac{n}{T} \log ^ 2 n)$的时间
  （注意可以用平衡树来维护块的序列，就能做到$O(\log n +T)$的修改复杂度）
• 如果我们能将原问题的每个操作转化成$f(n)$个dfs序的分裂、合并操作和$O(1)$个询问操作
• 那么将块状链表的每块大小设为$O(\sqrt{\frac{n \log ^ 2 n}{f(n)}})$， 每个操作的时间复杂度就是$O(\sqrt{n f(n) \log ^ 2 n})$

$f(n) = O(\log n)$！

• 假设树的形态不变，并且树根固定
• 我们用link-cut tree来维护这棵树的一个链剖分， 然后维护一个对应的dfs序列
• 在LCT access的过程中， 如果要将结点$x$的preferred-child改为$y$
• 就只要把子树$y$所对应的dfs序列的区间取出来，放到结点$x$后面
• 这样在access了结点$x$之后，根到$x$这条链在dfs序上是个区间， 子树$x$在dfs序上也是个区间


• 有换根操作怎么办？

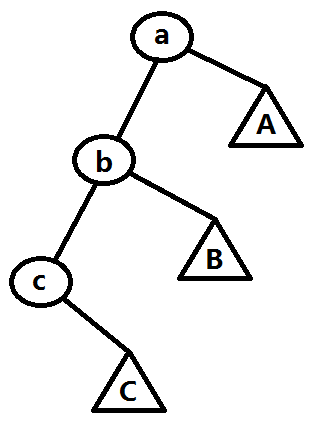
有换根操作怎么办？

其中椭圆表示结点，三角形表示子树 根为$a$时，这棵树的dfs序列为$a\ b\ c\ C\ B\ A$ 根为$c$时，这棵树的dfs序列为$c\ b\ a\ A\ B\ C$ 首先access新根，进行了$O(f(n))$次dfs序操作 然后只能用$O($树高$)$次dfs序操作来换根？

有换根操作怎么办？

不妨强行对原根到新根这条链所在的dfs序区间和dfs序剩下的部分打翻转标记 这样dfs序列就变成$c\ b\ a\ r(A)\ r(B)\ r(C)$了 注意有些子树的整个dfs序列都反了 我们在access的每一次循环中，检查一下是否发生了这种情况， 如果有的话，就用$O(1)$次dfs序的操作把这个子树的dfs序列翻转回去 于是对于树上的情况，我们就能做到$f(n) = O(\log n)$了！

仙人掌上的情况

• 我们用link-cut cactus来维护仙人掌的形态
• 于是跟上一题一样，一次操作可以转化成$O(\log n)$次树上的问题的操作
• $f(n) = O(\log ^ 2 n)$？
• 写个程序就会发现， $f(n)$更接近$O(\log n)$！
• 因为link-cut tree维护的是仙人掌的生成树，且维护时access到的点一样
• 于是在LCT上的链剖分与link-cut cactus维护的链剖分类似
• 那么在一次link-cut cactus的access中， 除了LCT的第一次access以外， 每一次LCT的access都只经过了$O(1)$条虚边， 这就说明了，LCT的access循环总次数是$O(\log n)$， 所以$f(n) = O(\log n)$
• 于是这题就在每个操作$O(\sqrt{n \log ^ 3 n})$的复杂度内解决了！

GL & HF